Thanks for the responses, folks.
Answer #2 was the one I was looking for, although as Billy and others have said there are elements of truth in 1 and 3 as we shall see.
Answer #4 was just thrown in for a laugh 
Let's dig deeper and see why Answer #2 was correct - remember I'm concentrating on HF:
Losses in a transmission lines come from 3 mechanisms:
1) Radiation Loss - the signal isn't fully contained by the line and some gets lost as radiation.
2) Copper Loss - the conductors have resistance, so when current flows they dissipate power. Basically the wires heat up.
3) Dielectric Loss - the insulation separating the conductors has RF voltage across it. Because the insulation is not a perfect dielectric, the RF voltage across it induces losses. Basically the insulation heats up.
At HF, even with ladderline, the Radiation Loss is tiny compared to Copper Loss or Dielectric Loss; so we can ignore it for this particular Puzzle.
Copper losses are caused by the AC resistance of the conductors; that resistance depends on the frequency because the skin depth varies with frequency. In fact the AC resistance rises as the square-root of the frequency because the skin depth decreases as the square-root of the frequency. So as we go from 7MHz to 28MHz (a factor of 4), the skin depth halves and the AC resistance will double.
On the other hand, Dielectric losses rise directly in proportion to frequency. So going from 7MHz to 28MHz causes them to increase 4-fold.
Mathematically we can express the loss as:
Total Loss = length*[k1*SQRT(f) + k2*f]
where k1 is a constant associated with the Copper loss and k2 is a constant associated with the Dielectric loss.
It's tempting to think that because the Dielectric loss increases faster than the Copper loss as we go up in frequency, it must therefore be the dominant loss. But that's not the case - it turns out that in typical transmission lines k2 is so small compared to k1 that it's the Copper losses that predominate until you get up into the UHF region.
Here's a graph plotting the Copper loss and Dielectric loss against frequency for a typical coax cable. You can see that the Copper loss predominates until we reach about 1GHz. Incidentally, also notice that the Copper losses in the coax centre conductor are higher than those in the braid - that's because the braid is larger diameter and has less AC resistance:
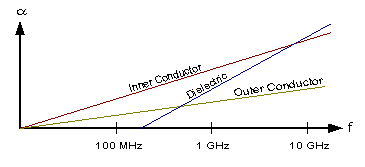
Hopefully you can see that Copper loss dominates at HF and it's the only loss we really need to consider for our Puzzle -
that rules out Answer #3.
-------------------------------------------------------------------------------------------------------------------------
At this stage we could be forgiven for thinking that Answer #1 is correct - after all, if it's Copper loss which matters most, and if Copper loss depends on conductor resistance, surely conductor diameter must be the predominant factor! Well, I just measured the diameter of the copper conductor in some commercial 450ohm ladderline in my shack: it was 1mm. Then I measured the diameter of the inner conductor of some RG213: it was 2.3mm. So, how come the cable with the thicker wire has the higher matched losses?
Let's take two identical lengths of transmission line carrying 150W; each line is matched with a load equal to its characteristic impedance. In the case of the RG213 the current will be:
I = SQRT(P/R) = SQRT(150/50) = 1.7A
and in the case of the ladderline it will be:
I = SQRT(P/R) = SQRT(150/450) = 0.57A
Now let's assume that the AC resistance of one ladderline wire is 1ohm for this particular length of line; we would then expect the AC resistance of the RG213 inner conductor to be about 2.3 times less: 0.43ohms. So now we can work out the power loss for one leg of the ladderline:
P = I^2*R = 0.57*0.57*1 = 0.32W
and for the inner conductor of the RG213:
P = I^2*R = 1.7*1.7*0.43 = 1.24W
So,
even though the RG213 conductor resistance is lower, the fact that it is carrying higher current makes its losses higher ! [Strictly we ought to double the loss for the ladderline becasuse there are 2 wires, and increase the loss for the RG213 to account for the loss in the braid, but we will reach exactly the same conclusion].
To summarise:
the higher characteristic impedance of the ladderline means it needs to pass less current for a given power, and that results in lower losses - making Answer #2 the correct one. This should sound familiar - the National Grid distributes power at high-voltage/low-current to reduce copper losses in the wires; a high characteristic impedance transmission line is doing exactly the same thing.
There's an interesting observation that follows from this: if I take the wires forming my 450 ohm ladderline and move them farther apart until I increase the characteristic impedance to 600ohms, the matched loss will be lower even though the wire resistance is
exactly the same.
-------------------------------------------------------------------------------------------------------------------------
Finally, and just for fun, now we understand the loss mechanisms a bit better let's try to work out from "first principles" the actual matched loss of 100m of my commercial 450 ohm ladderline at 10MHz - it's not "rocket science"!
What's the resistance of the wire:
* I measured the wire diameter as 1mm
* The "skin depth" for copper at 10MHz is 21um
* So the cross-sectional area of copper that the signal is flowing through is Pi*1mm*0.021mm = 0.066 sq.mm:
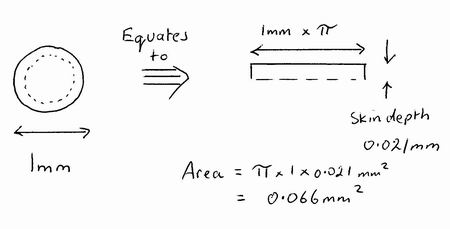
* The resistivity of copper is 1.72*10^-8 ohm.metres
* So the resistance of 100m of 1mm diameter wire @ 10MHz is 100*1.72/6.6 = 26ohms
* But the ladderline is made up of two wire, so the total resistance is 52ohms
So, what's the loss:
* Firstly note that "450ohm" commercial ladderline actually has a characteristic impedance closer to 400ohms
* Assume that 400W is applied to the line: then the current flowing is 1A
* Therefore the total copper loss must be I*I*R = 1*1*52 = 52W
* So, for 400W input to the line, 348W reaches the other end.
* Therefore the loss in dB is 10*log(348/400) = 0.6dB
Compare that with the published figure for 100m of Wireman 553 ladderline @ 10MHz of 0.67dB ... not far out ..... phew .... QED
------------------------------------------------------------------------------------------------------------------------
Conclusion: if we're looking for low matched-loss HF transmission line we should be looking for one with a high characteristic impedance and large diameter conductors; of the two, a higher characteristic impedance has the greater impact.
Finally, finally, please note that I've been talking about
"matched loss"; we quite often use ladderline under unmatched conditions - for example when feeding a muliband doublet - and that introduces other factors which I'll touch on in a Part 2.
73,
Steve G3TXQ


